8  Seaborn for data visualisation

Seaborn is a Python data visualisation library based on Matplotlib. Seaborn makes it easy to create attractive and well-laid-out plots. Seaborn also plays nicely with Pandas data structures, which is important for data science related visualizations. We can install Seaborn easily using pip or conda:

# installation using pip
pip install seaborn

8.1 Getting started

Let’s start by creating a simple scatter plot using Seaborn. We start by importing Seaborn for the visualizations and Numpy and Pandas for generating and handling the data.

import seaborn as sns
import numpy as np
import pandas as pd

Next, we generate some random data and plot it using Seaborn (Figure 8.1).

x = np.random.normal(size=100)
y = np.random.normal(size=100)
df = pd.DataFrame({'x': x, 'y': y})

sns.scatterplot(x='x', y='y', data=df)

Figure 8.1: Scatter plot created using Seaborn.

We can see right away that Seaborn’s syntax differs somewhat from the one used by Matplotlib.

Seaborn Documentation

The Seaborn website contains something called the API reference, which is a comprehensive guide to the functions and classes in Seaborn. It is a great resource to learn more about the details regarding Seaborn and how to use it effectively. You can find it at https://seaborn.pydata.org/api.html.

8.2 Evaluating distributions

Seaborn offers many convenient plotting functions for evaluating distributions. Let’s explore the penguins dataset that comes with Seaborn. The penguins dataset contains data on the size and species of penguins collected from different islands in the Palmer Archipelago, Antarctica. We can load the dataset using the following code:

penguins = sns.load_dataset('penguins').dropna()

penguins.head()

Table 8.1: The first few rows of the penguins dataset.

	species	island	bill_length_mm	bill_depth_mm	flipper_length_mm	body_mass_g	sex
0	Adelie	Torgersen	39.1	18.7	181.0	3750.0	Male
1	Adelie	Torgersen	39.5	17.4	186.0	3800.0	Female
2	Adelie	Torgersen	40.3	18.0	195.0	3250.0	Female
4	Adelie	Torgersen	36.7	19.3	193.0	3450.0	Female
5	Adelie	Torgersen	39.3	20.6	190.0	3650.0	Male

Table 8.2 shows a summary of the dataset.

penguins.describe()

Table 8.2: Summary statistics for the penguins dataset.

	bill_length_mm	bill_depth_mm	flipper_length_mm	body_mass_g
count	333.000000	333.000000	333.000000	333.000000
mean	43.992793	17.164865	200.966967	4207.057057
std	5.468668	1.969235	14.015765	805.215802
min	32.100000	13.100000	172.000000	2700.000000
25%	39.500000	15.600000	190.000000	3550.000000
50%	44.500000	17.300000	197.000000	4050.000000
75%	48.600000	18.700000	213.000000	4775.000000
max	59.600000	21.500000	231.000000	6300.000000

8.2.1 Pairplot

The pairplot() function creates a grid of scatterplots for all pairs of numerical columns in a DataFrame. Additionally, it show’s an estimate of the distribution of each column along the diagonal. It is simple yet effective way to get an overview of your data, provided the data doesn’t entail a huge number of numeric columns. Figure 8.2 shows an example for the penguins dataset.

pen_plt = sns.pairplot(penguins, hue='island')
pen_plt.fig.set_size_inches(7,7)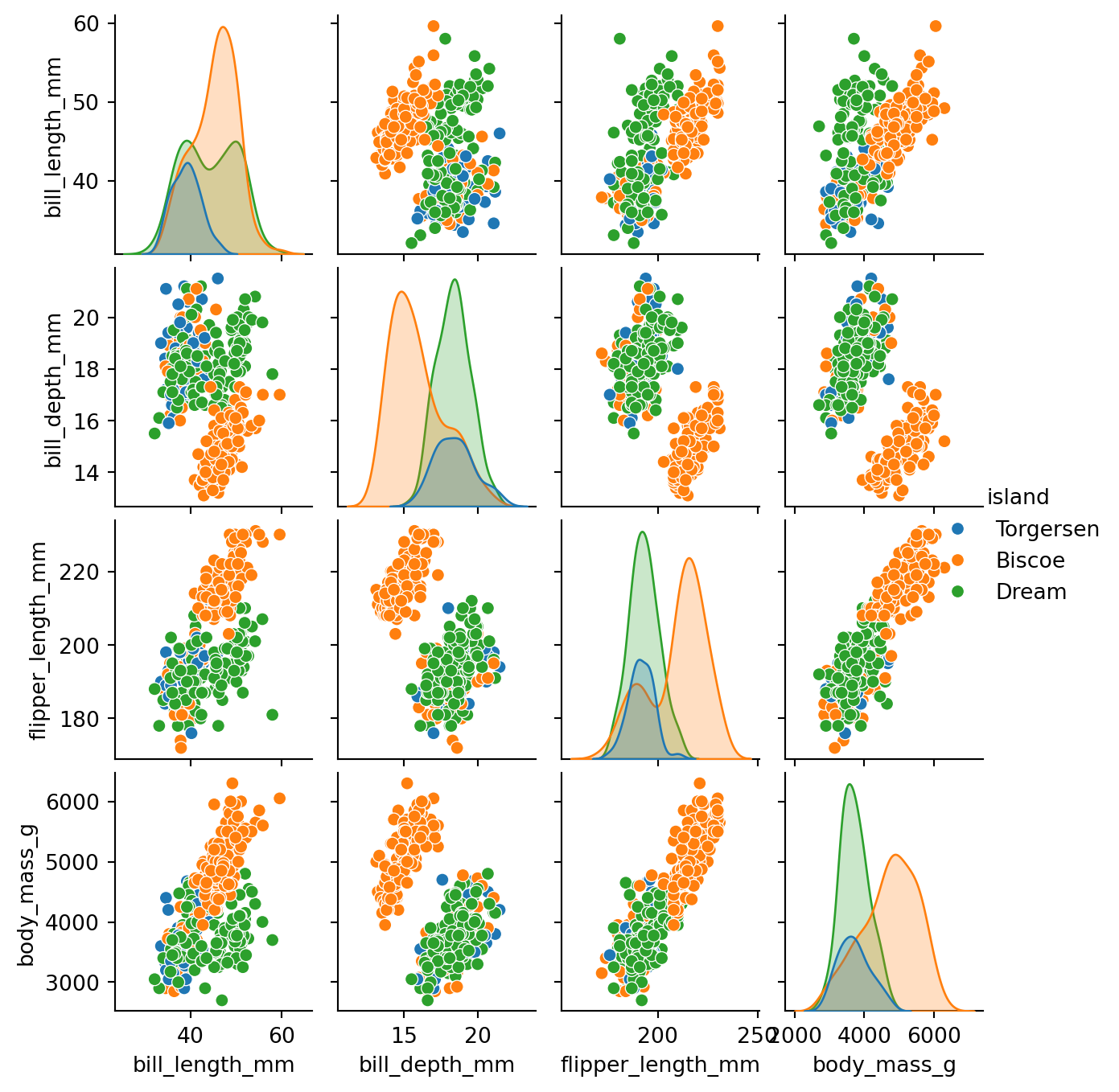

Figure 8.2: Pairplot of the penguins dataset.

Above we used the hue parameter to color the points based on the island where the penguins were observed. This makes it easier to see if there are any differences between the islands. We can set the hue parameter to any categorical column in the dataset.

8.2.2 Displot & Histogram

The displot() function creates a histogram and a kernel density estimate of the data. It is a convenient way to evaluate the distribution of a single variable. Figure 8.3 shows an example for the penguins dataset.

sns.displot(penguins['flipper_length_mm'], kde=True)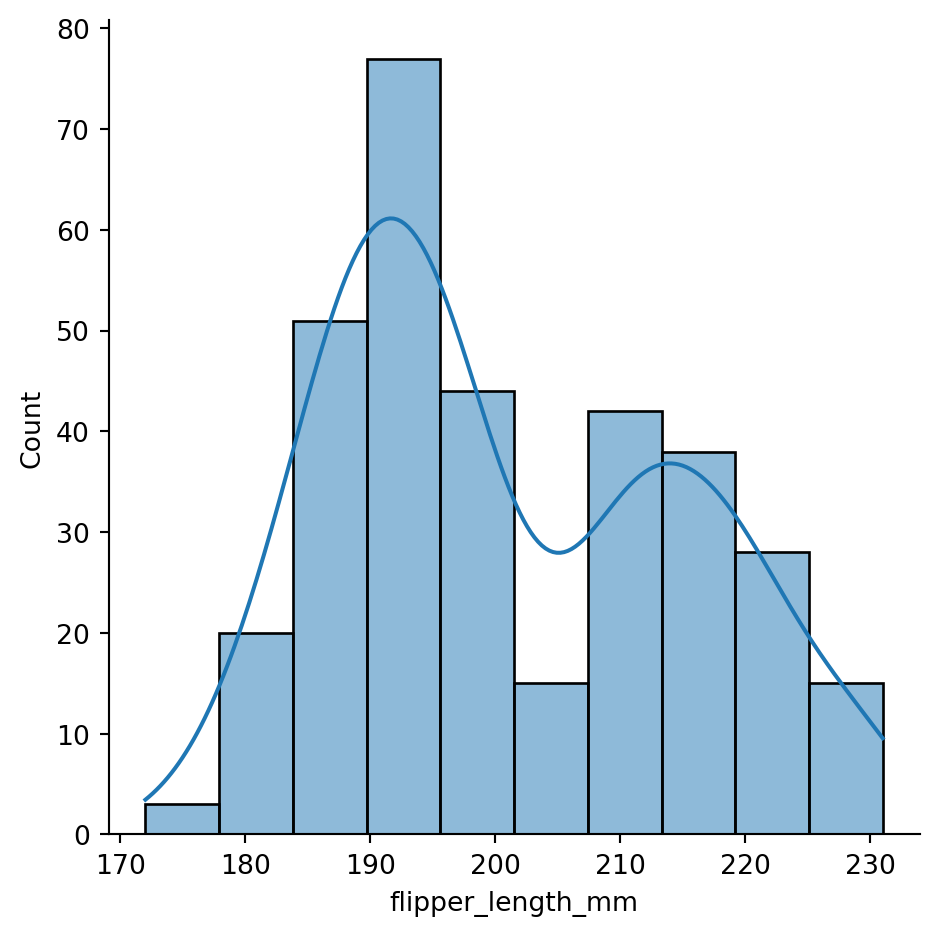

Figure 8.3: Distribution plot of the penguin’s flipper length.

If we are simply looking to create a histogram, we can use the histplot() function. Figure 8.4 shows an example for the penguins dataset.

sns.histplot(penguins['flipper_length_mm'], bins=20)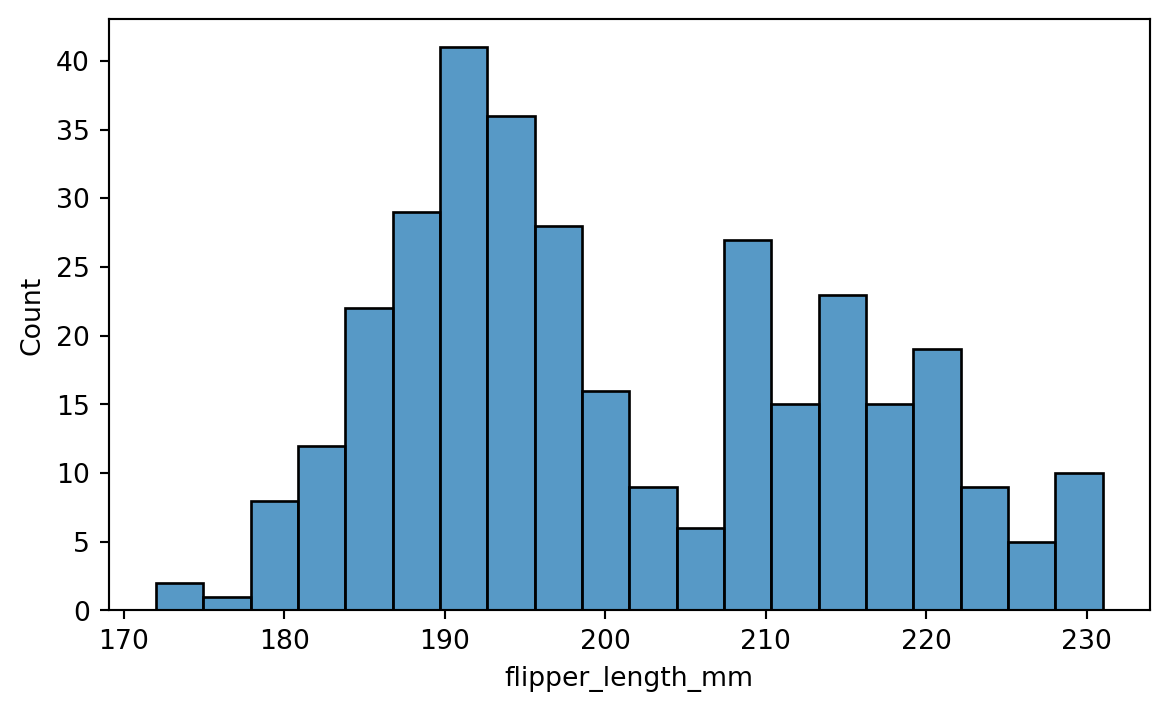

Figure 8.4: Histogram of the penguin’s flipper length.

Here we used the bins parameter to set the number of bins in the histogram. There are many other parameters that can be used to customize the plot, including but not limited to:

• binwidth: Width of each bin
• fill: Whether to fill the bars with color.

8.2.3 Boxplot

Boxplot is convenient for visualizing the distribution of a numerical variable across different categories. The boxplot() function creates a boxplot of the data. Figure 8.5 shows an example for the penguins dataset.

sns.boxplot(x='species', y='flipper_length_mm', data=penguins)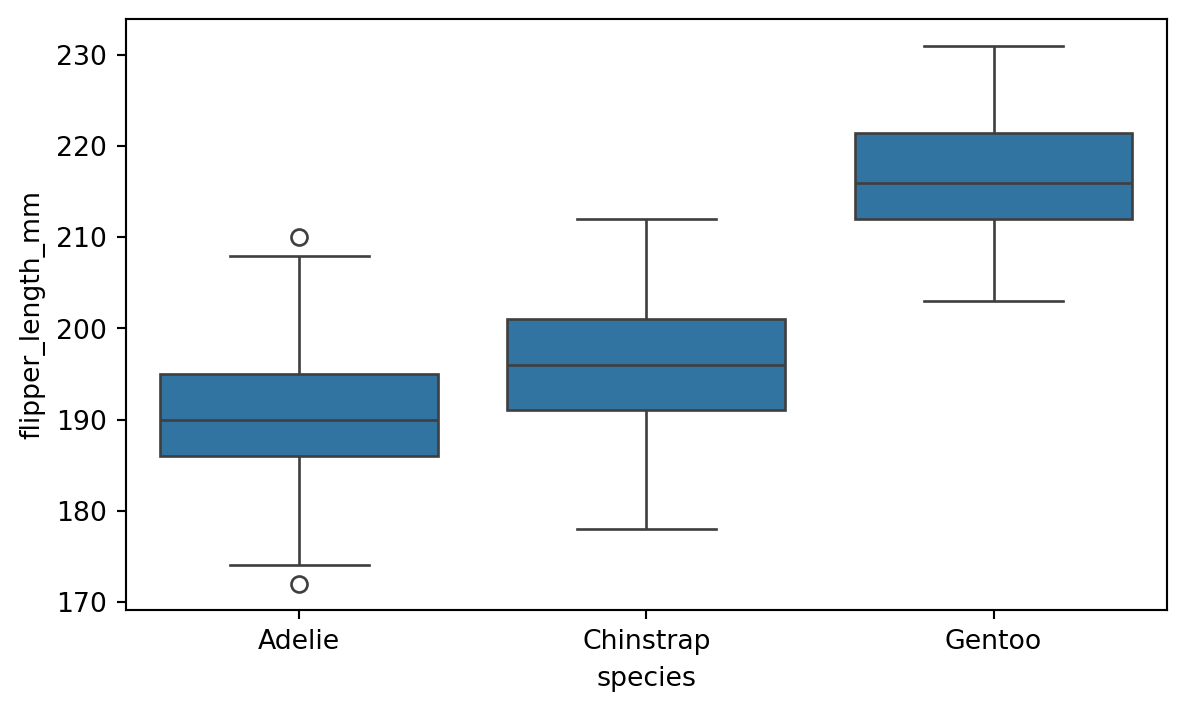

Figure 8.5: Boxplot of the penguin’s flipper length. The box shows the positions of the first, second (median), and third quartiles. The whiskers extend to the most extreme data points not considered outliers (according to normal distribution), and the outliers are plotted as individual points.

8.2.4 Jointplot

The jointplot() function creates a scatter plot of two numerical variables along with the histograms of each variable. It is a convenient way to visualize the relationship between two variables. Figure 8.6 shows an example with the flipper length and body mass.

sns.jointplot(x='flipper_length_mm', y='body_mass_g', 
data=penguins, kind='reg')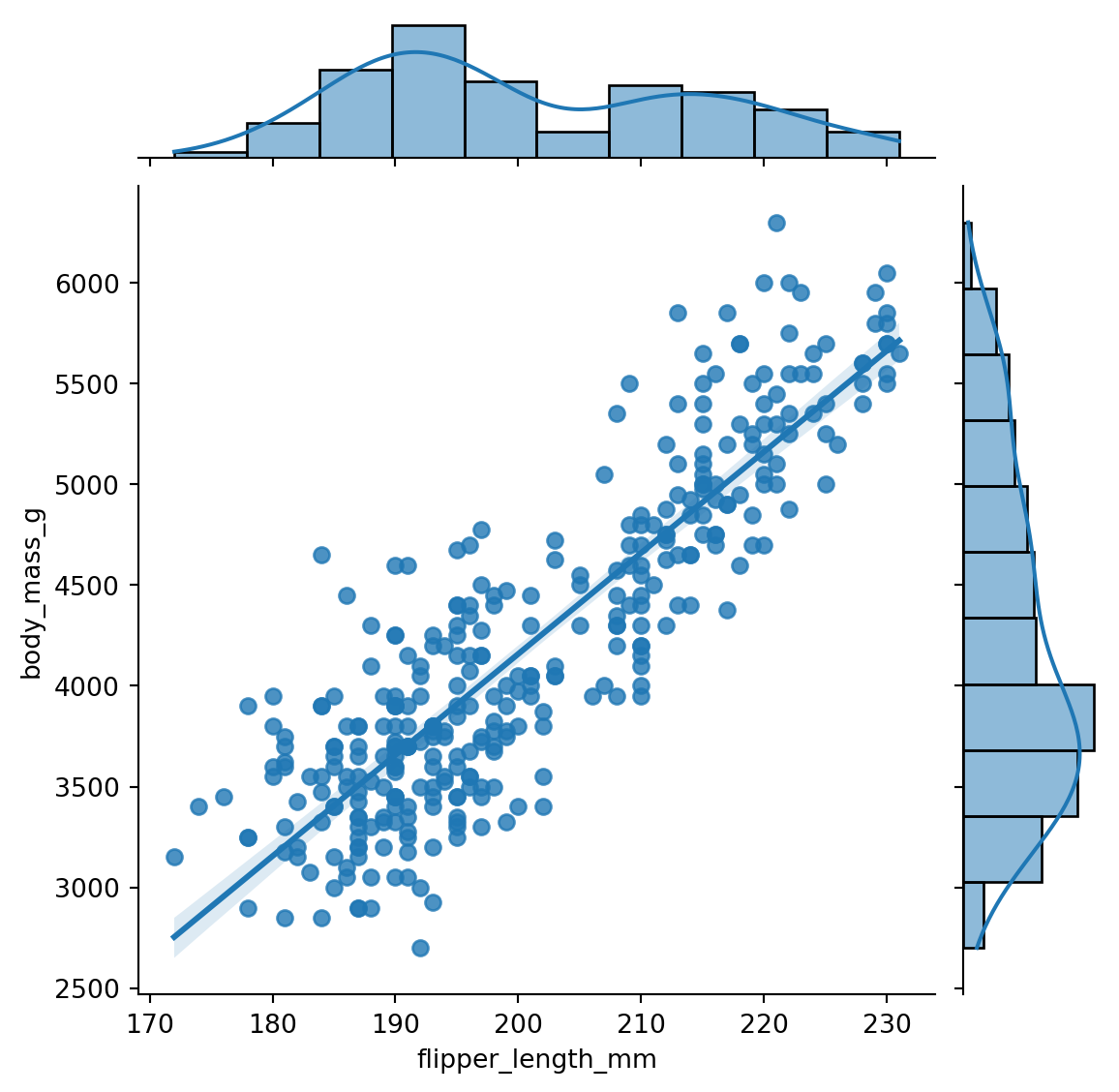

Figure 8.6: Jointplot showing the correlation between penguin flipper length and body mass.

The kind parameter is very useful, as it allows us to choose the type of plot to display in the jointplot. For example, if we have a lot of points we can use kind='hex' to create a hexbin plot. Figure 8.7 shows an example.

sns.jointplot(x='flipper_length_mm', y='body_mass_g',
data=penguins, kind='hex')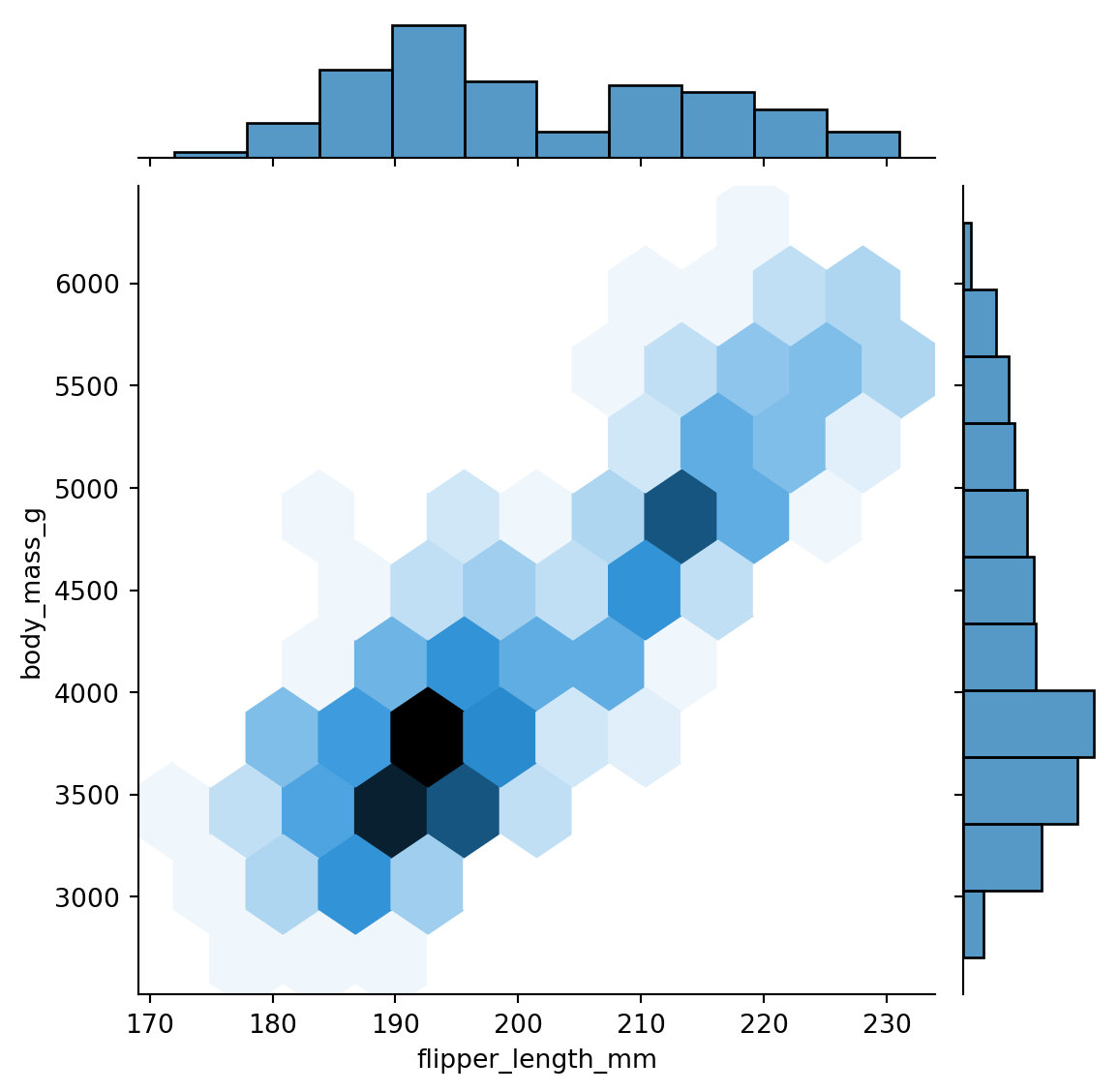

Figure 8.7: Jointplot showing the correlation between penguin flipper length and body mass using a hexbin plot. The number of observations within each hexagon is represented by the color intensity.

8.3 Comparing groups

A common task in data analysis is to compare different groups within data. For example, in the penguins dataset we might want to compare the body mass of the different species. One way to do this is to create a barplot, as we have done in Figure 8.8.

sns.barplot(x='species', y='body_mass_g', data=penguins)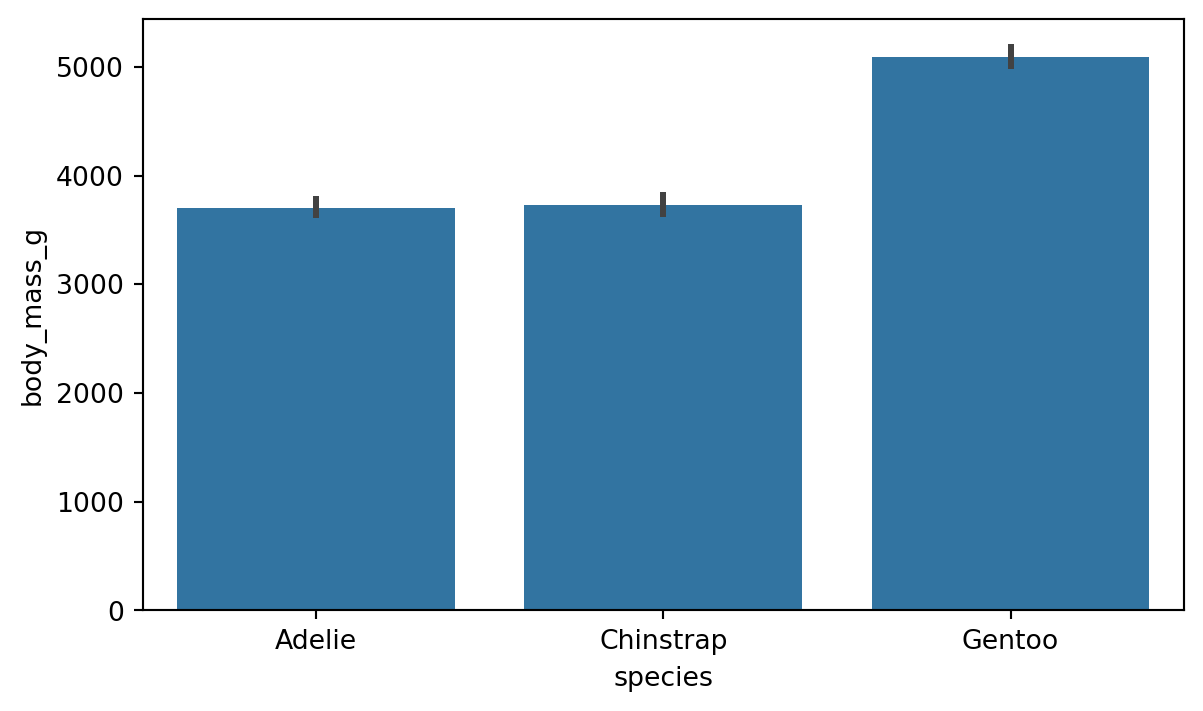

Figure 8.8: Barplot showing the average body mass of the different penguin species.

By default, the barplot shows the average value of the y variable for each category in the x variable. The barplot function has a parameter for adjusting which estimator is used in comparing the group. We change the estimator to e.g. median quite easily with the help of numpy as shown in Figure 8.9.

import matplotlib.pyplot as plt

plot = sns.barplot(x='species', y='body_mass_g', data=penguins, estimator=np.median)
# re-label y-axis
plot.set_ylabel('Median body mass (g)')

plt.show()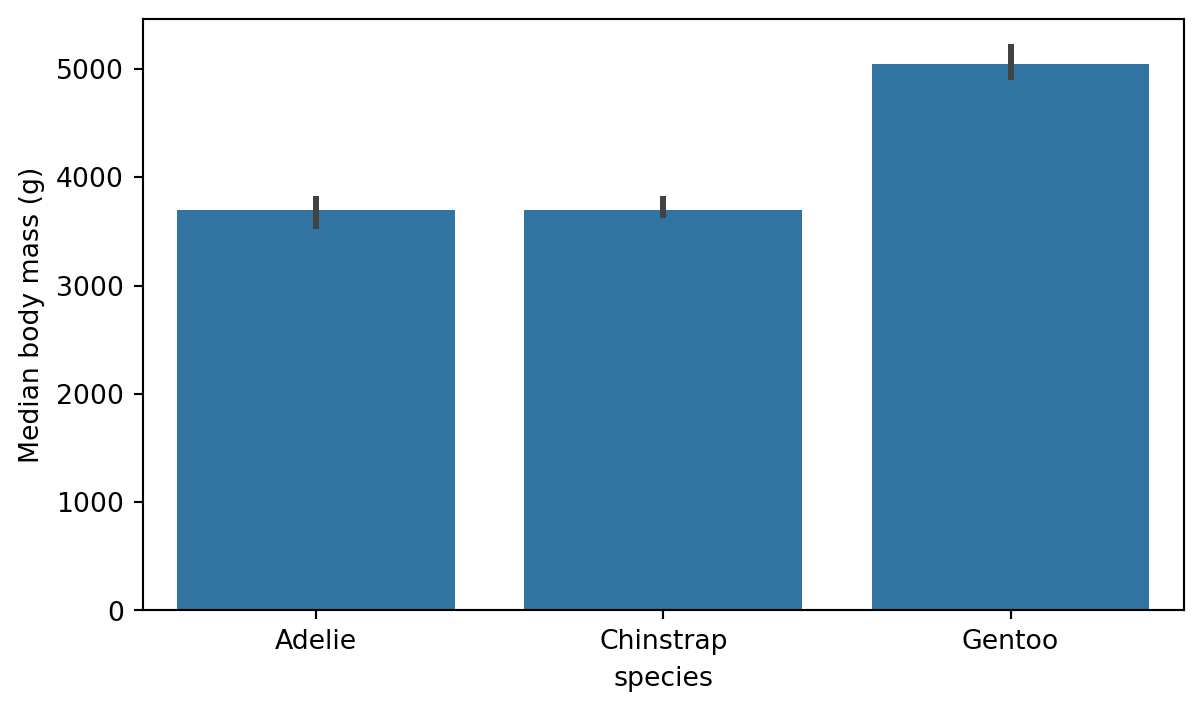

Figure 8.9: Barplot showing the median body mass of the different penguin species.

8.3.1 Countplot

If the bars in the barplot are used for counting the number of observations, we can use the countplot() function in Seaborn. Figure 8.10 shows an example of this on the number of different species in the penguins dataset. This is a great way of assessing if the dataset is balanced or not.

sns.countplot(x='species', data=penguins)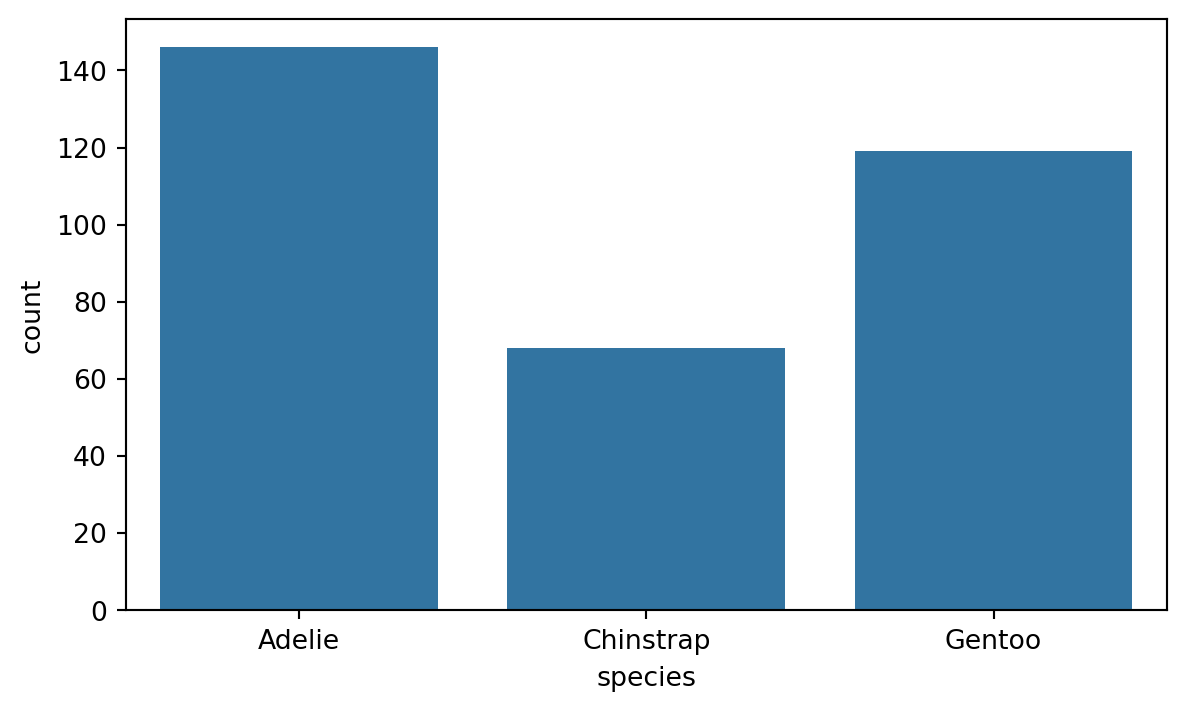

Figure 8.10: Countplot showing the number of penguin observations per species in the data.

8.3.2 Digging deeper with the hue parameter

As we saw above, the countplot and barplot functions are effective tools for comparing groups within a dataset. The hue parameter allows us to add an extra layer of granularity to the plot. For example, we can use the hue parameter to compare the bill lenght of the different species of penguins and see the effect of sex of the penguin. Figure 8.11 shows an example of this.

sns.barplot(x='species', y='bill_length_mm', hue='sex', data=penguins)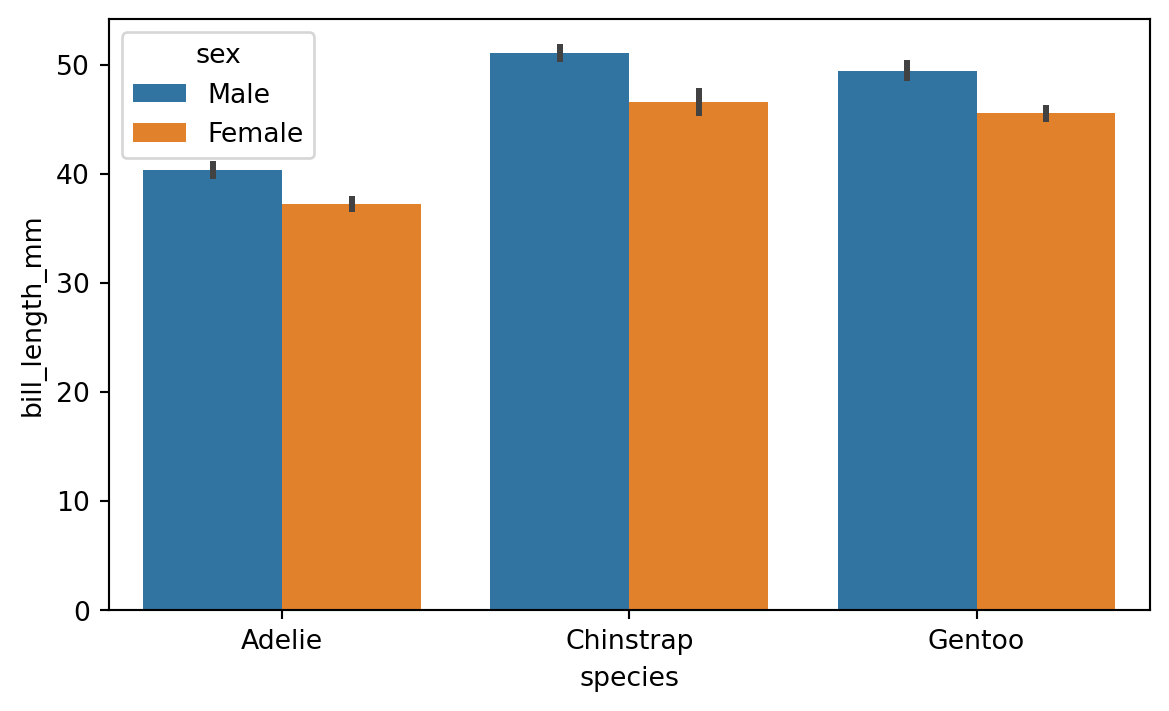

Figure 8.11: Barplot showing the average bill length of the different penguin species. The bars are colored according to sex.

Using the hue parameter is very useful also with plot types like boxplot and violinplot, which display distributions. Figure 8.12 shows an example of a boxplot with the hue parameter.

sns.boxplot(x='species', y='flipper_length_mm', hue='sex', data=penguins)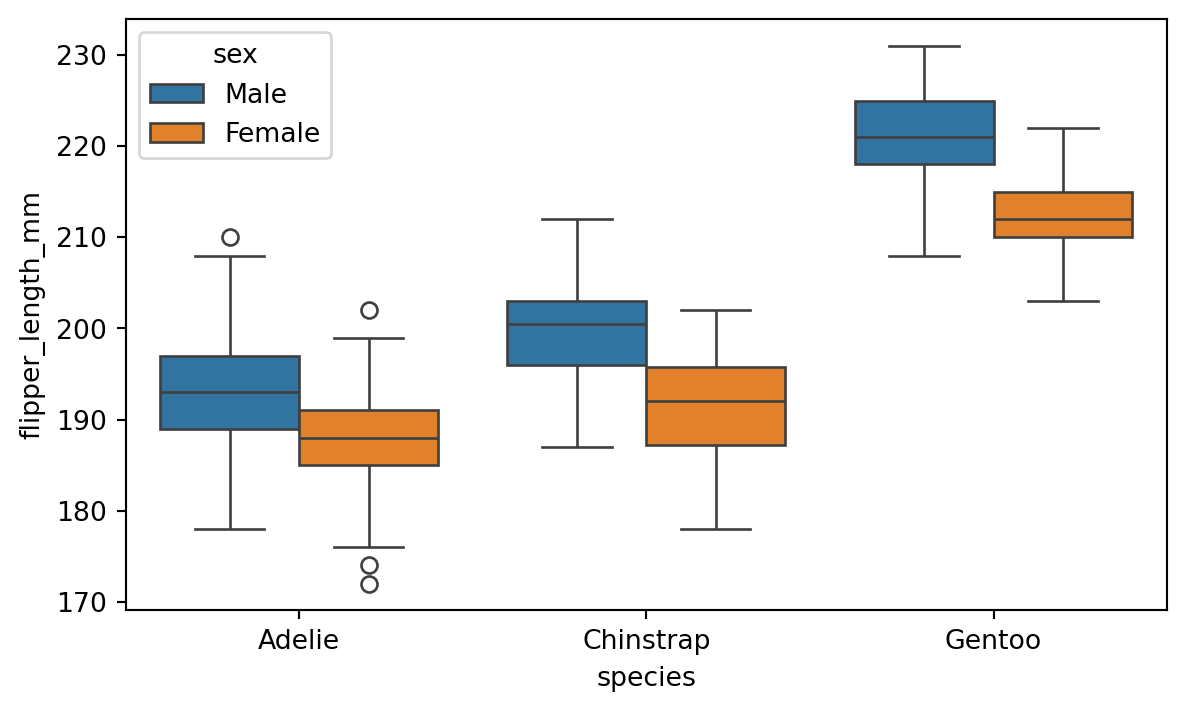

Figure 8.12: Boxplot showing the flipper length of the different penguin species. The boxes are colored according to sex.

8.4 Faceting

In the previous section we saw how to utilize the hue parameter in separating data based on a grouping variable. Another useful technique for visualizing grouped data is faceting. We can use the FacetGrid class to create a separate histogram for each species in the penguins dataset. Figure 8.13 shows an example of this.

g = sns.FacetGrid(penguins, col='species')
g.map(sns.histplot, 'flipper_length_mm')
g.fig.set_size_inches(w=7, h=3)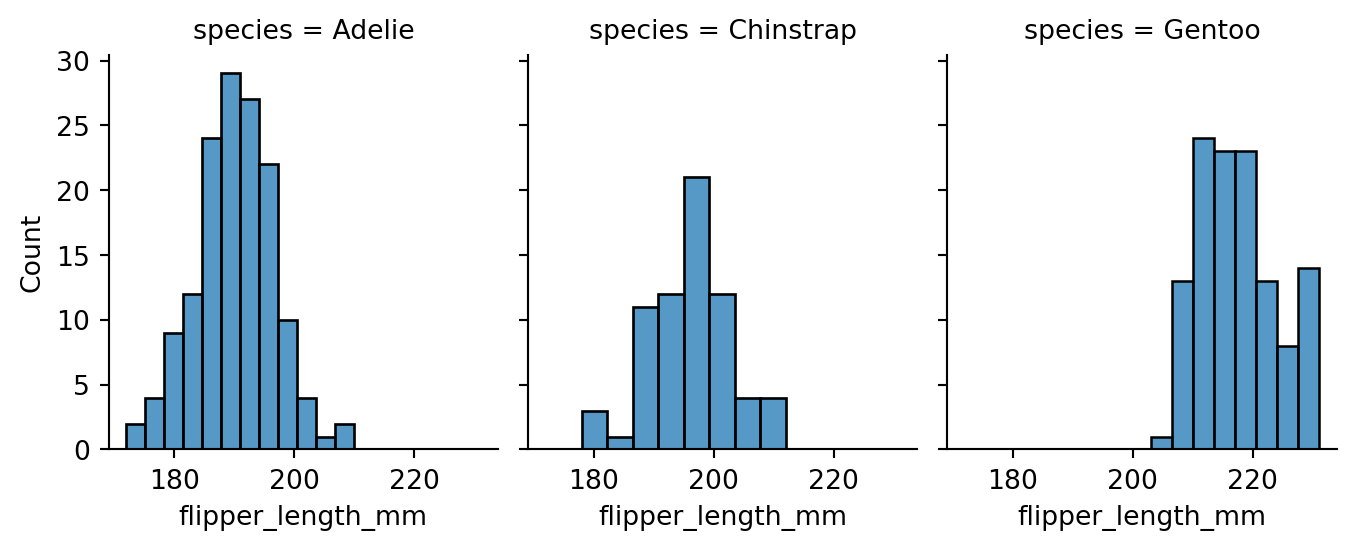

Figure 8.13: FacetGrid showing the distribution of flipper length for each penguin species. By setting the species column as the col parameter value, separate plots for each species are created into their respective columns.

We can also use the row parameter to facet the plots into rows. This is especially useful when we have two categorical columns we want to group by. Figure 8.14 shows data grouped by the species and sex variables.

# modify the sex column to show F for Female and M for Male
penguins['sex'] = penguins['sex'].apply(lambda x: 'F' if x == 'Female' else 'M')

g = sns.FacetGrid(penguins, row='sex', col='species')
g.map(sns.scatterplot, 'bill_length_mm', 'bill_depth_mm')
g.figure.set_size_inches(w=7, h=6)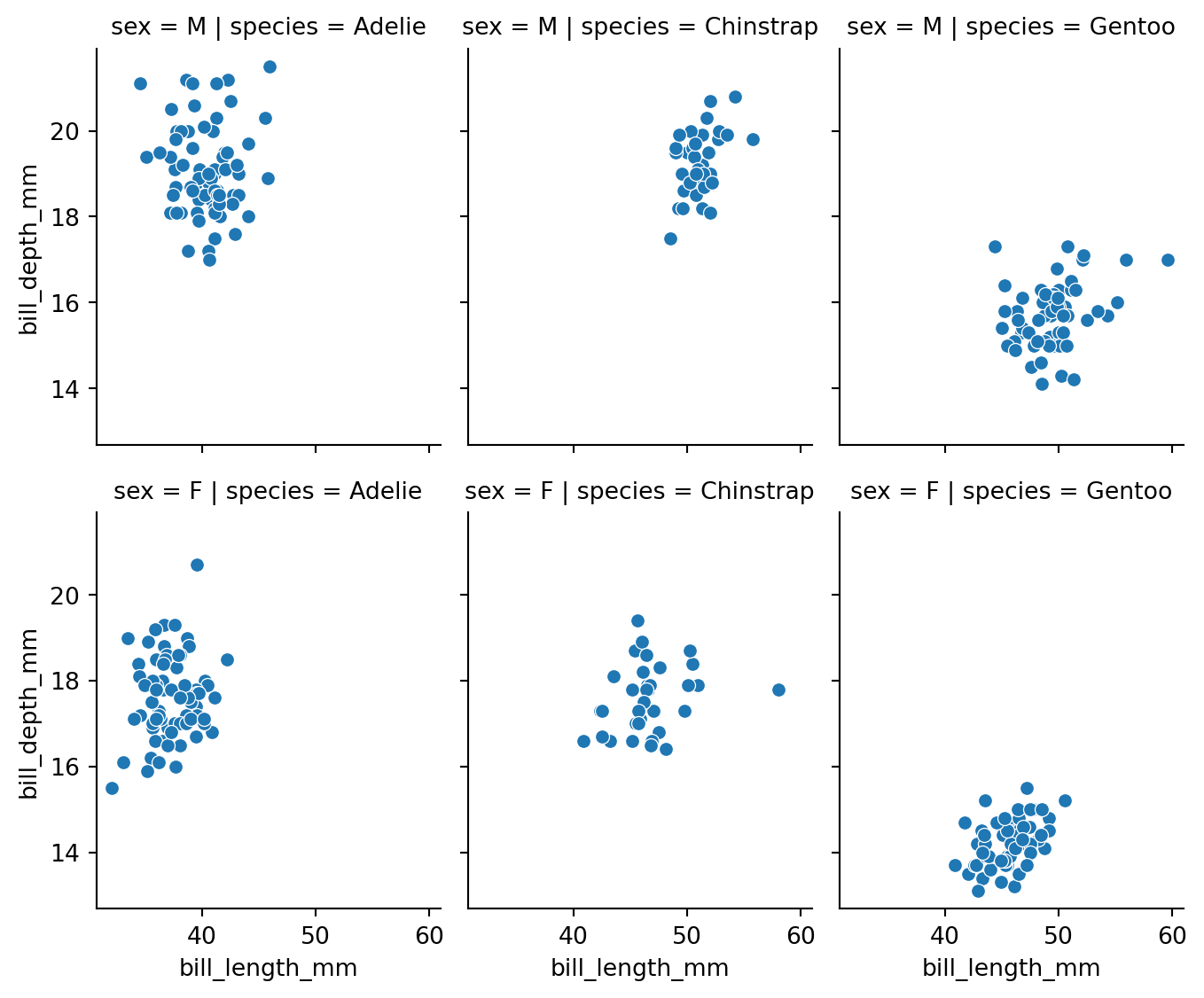

Figure 8.14: FacetGrid showing the correlation of bill length and bill depth for each penguin species. The plots are faceted into rows based on sex.

8.4.1 More complex Grids

FacetGrid is not the only way to create a grid of plots in Seaborn. The pairplot function we saw earlier is another example of a grid of plots. In fact pairplot is just a specialized version of a more general function called PairGrid. We can use PairGrid to create a grid of plots for any pair of variables in the dataset, and we can also specify which type of plots we want on different parts of the grid. Figure 8.15 shows an example of this.

g = sns.PairGrid(penguins, hue='species')
# set the upper triangle to scatterplot
g.map_upper(sns.scatterplot)
# set the lower triangle to kdeplot
g.map_lower(sns.kdeplot)
# set the diagonal to histplot
g.map_diag(sns.histplot)
g.add_legend()
sns.move_legend(g, "lower center",
    bbox_to_anchor=(.5, 1), ncol=3, title=None, frameon=False
    )

# set figure size
g.figure.set_size_inches(w=6, h=6)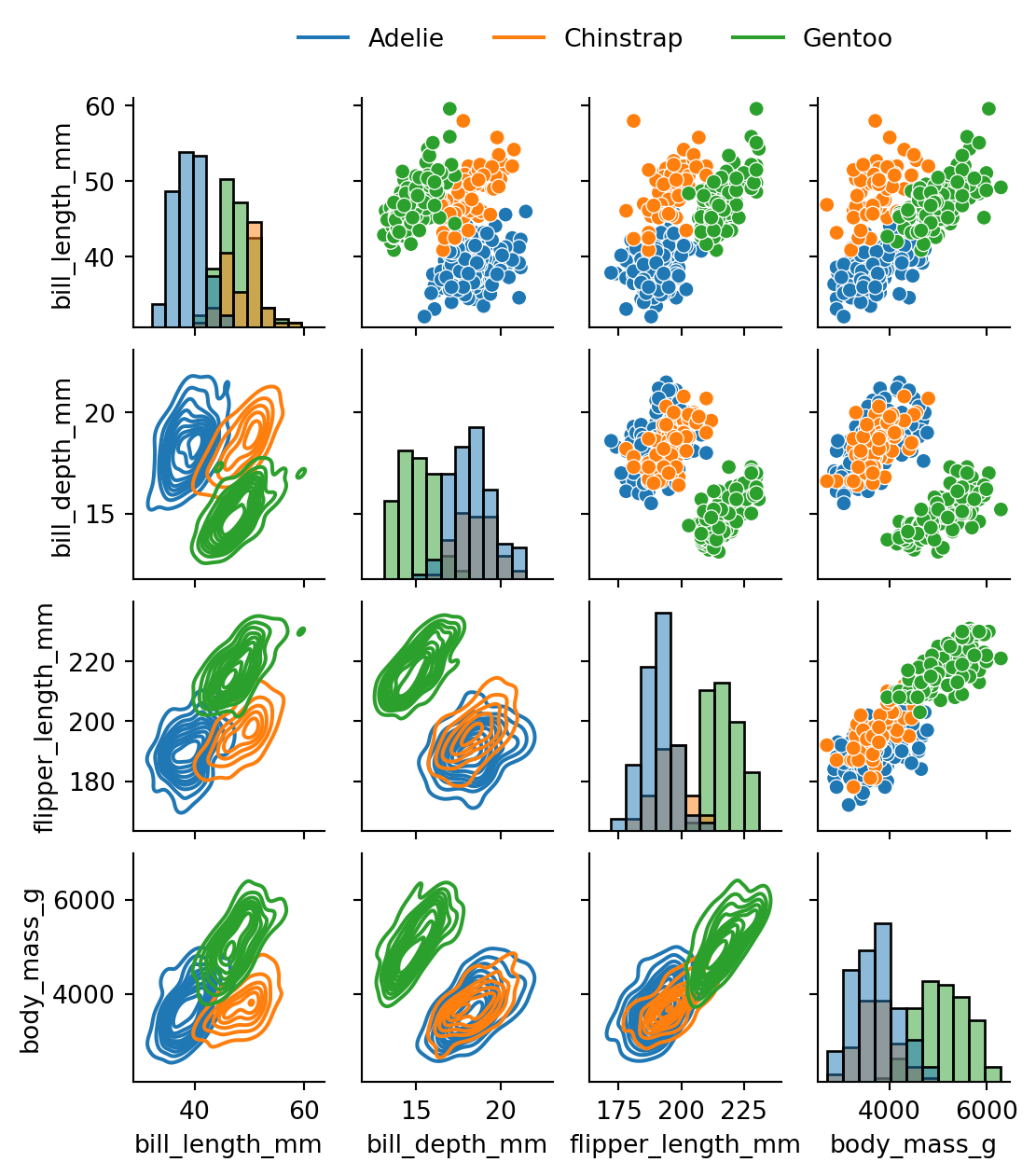

Figure 8.15: PairGrid showing the pairwise relations of all numeric variables in the penguins dataset.

8.5 Visualizing Correlation

Correlation can be roughly described as a measure of the strength and direction of a linear relationship between two numerical variables. For example, for the numeric columns in the penguins dataset, we can calculate the correlation matrix using the corr() function. Table 8.3 shows the correlation matrix for the penguins dataset.

pen_corr = penguins.corr(numeric_only=True)
pen_corr

Table 8.3: A matrix showing the Pearson correlation between the numerical columns in the penguins dataset.

	bill_length_mm	bill_depth_mm	flipper_length_mm	body_mass_g
bill_length_mm	1.000000	-0.228626	0.653096	0.589451
bill_depth_mm	-0.228626	1.000000	-0.577792	-0.472016
flipper_length_mm	0.653096	-0.577792	1.000000	0.872979
body_mass_g	0.589451	-0.472016	0.872979	1.000000

Once we have our data in this rectangular form, we can use the heatmap() function, which offers a convenient way to visualize the correlation. The heatmap() function creates a color-coded matrix that shows the correlation between each pair of variables. Figure 8.16 shows an example of this for the correlation data we created above.

sns.heatmap(pen_corr, annot=True)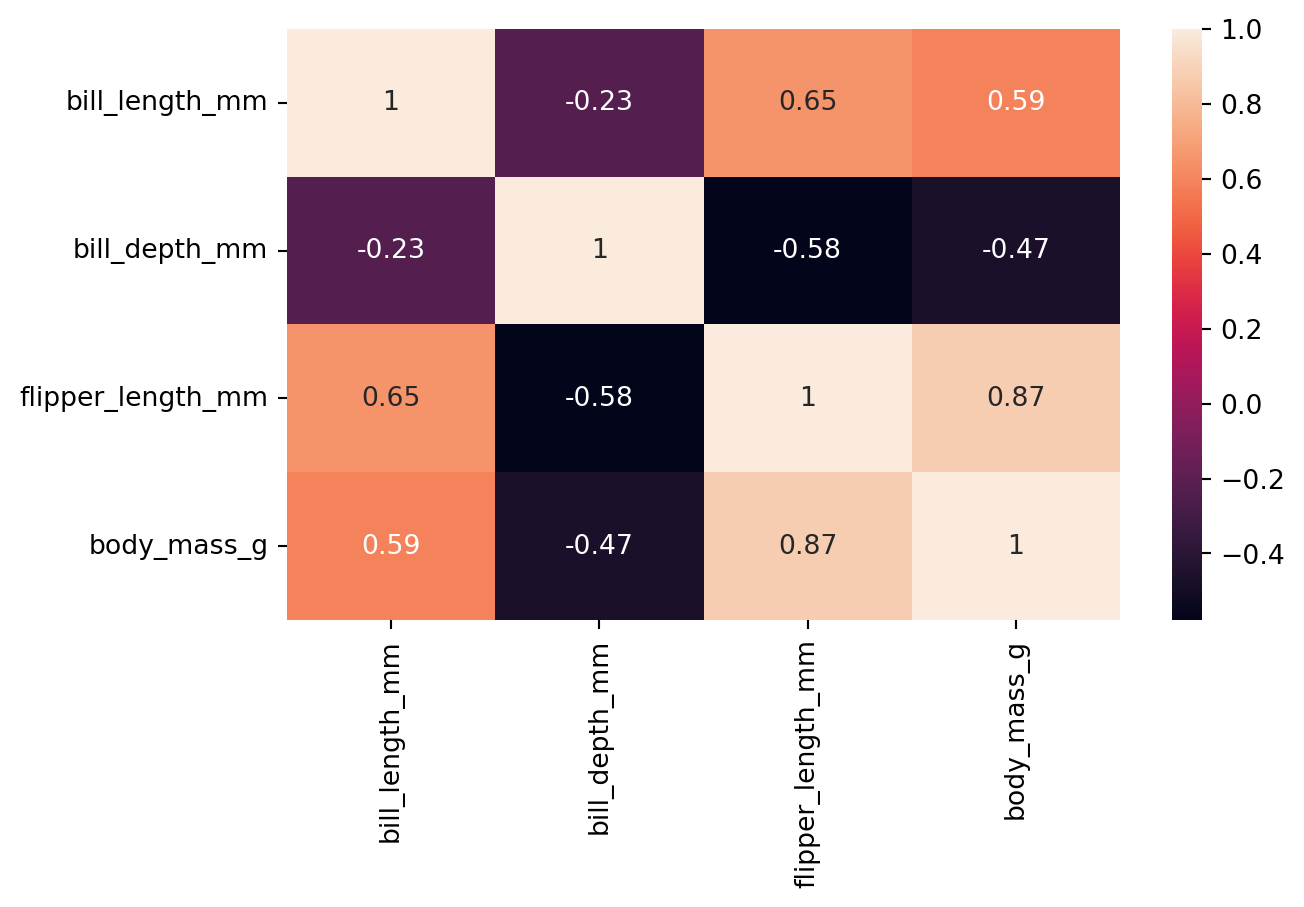

Figure 8.16: Heatmap showing the correlation between numerical variables in the penguins dataset. Color intensity is used to visualize the correlation values.

The annot parameter is used to display the numeric correlation values in the heatmap. Moreover, cmap parameter can be used to change the color map of the heatmap.

8.5.1 Heatmap for temporal data

Heatmaps can also be used to visualize temporal data. Table 8.4 shows monthly weather data from the website Our World in Data.

weather = pd.read_csv('data/monthly-average-surface-temperatures-by-year.csv')
weather

Table 8.4: The finnish weather dataset from Our World in Data.

	Entity	Code	Year	2024	2023	2022	2021	2020	2019	2018	...	1959	1958	1956	1954	1952	1957	1955	1953	1951	1950
0	Finland	FIN	1	-12.356432	-4.536643	-7.592226	-9.110156	-3.112542	-11.025353	-6.895465	...	-9.696966	-12.954665	-11.878848	-8.946227	-5.870114	-6.206512	-9.807618	-9.158957	-10.899360	-14.994019
1	Finland	FIN	2	-7.631946	-5.592857	-6.273704	-11.295887	-4.104153	-5.959055	-11.653291	...	-4.385164	-11.575406	-16.195097	-13.229277	-5.858663	-6.452776	-13.163642	-13.099696	-8.866541	-8.616582
2	Finland	FIN	3	-2.152660	-6.260747	-2.362002	-3.575844	-2.093242	-3.754119	-8.216735	...	-1.374446	-9.041509	-6.101201	-3.394979	-9.736150	-8.902771	-8.678738	-3.652206	-7.219227	-4.774562
3	Finland	FIN	4	-0.105814	1.859364	0.963580	1.959561	0.592504	3.668244	1.857609	...	0.429239	-1.223686	-2.926554	-0.158412	1.350001	-0.055782	-3.018537	2.357863	1.580248	2.926893
4	Finland	FIN	5	10.342938	9.054110	7.681894	7.209668	6.447229	7.416959	11.818787	...	7.576959	5.305153	7.060782	9.387682	5.249408	6.424380	3.803955	7.328690	4.187241	6.869668
5	Finland	FIN	6	15.629230	14.390386	14.857914	16.784351	16.298048	14.332166	12.409929	...	13.862224	12.240686	14.262403	12.196805	12.959100	10.485080	10.143443	16.841997	11.469393	13.351920
6	Finland	FIN	7	17.379380	15.121183	16.573692	18.357800	14.814271	14.564145	19.720356	...	16.012850	13.836065	14.284949	16.679026	14.955886	17.375101	16.000717	15.119339	13.776219	14.620484
7	Finland	FIN	8	15.999804	15.713537	15.900022	13.261284	14.121853	13.773454	15.358797	...	14.763309	13.833643	11.212431	13.601360	11.714494	13.959742	15.751595	13.766891	16.507440	15.331268
8	Finland	FIN	9	NaN	12.078142	7.694565	7.075720	9.989091	8.631719	10.090892	...	6.644055	8.106494	6.433380	9.015210	6.523679	7.595360	10.376423	6.875361	9.839784	9.541843
9	Finland	FIN	10	NaN	0.258406	4.493286	4.510300	4.983604	1.240841	3.102760	...	2.086031	3.264047	0.802558	1.842529	-0.712148	2.896886	1.894943	4.152942	5.239940	4.349140
10	Finland	FIN	11	NaN	-5.321711	-1.655154	-2.792642	1.341732	-3.120430	0.699558	...	-2.421227	0.332971	-8.738729	-3.450766	-4.315333	-2.058513	-6.467130	-0.935875	-4.115920	-2.016795
11	Finland	FIN	12	NaN	-8.636971	-6.510187	-9.504569	-2.615182	-2.354235	-5.373116	...	-9.508020	-11.801905	-6.794479	-2.086087	-7.242684	-6.743253	-16.398590	-2.729617	-4.081283	-5.246907

12 rows × 78 columns

We can see that the dataset contains the average temperature for each month in Finland from 1950 to 2024. We can use the heatmap() function to visualize this data. When we look at the data in Table 8.4 we notice that the months are actually listed under the Year column, while the years themselves are listed with numeric column names. First thing to do, is to move the Year column as the index and remove the Entity and Code columns. Finally, we shall transpose the data, so that the months will be displayed on the x-axis of the resulting heatmap (Figure 8.17).

weather = weather.set_index('Year').drop(columns=['Entity', 'Code'])
# rename index to month
weather.index.name = 'Month'
# transpose the data
weather = weather.T
sns.heatmap(weather, cmap='coolwarm')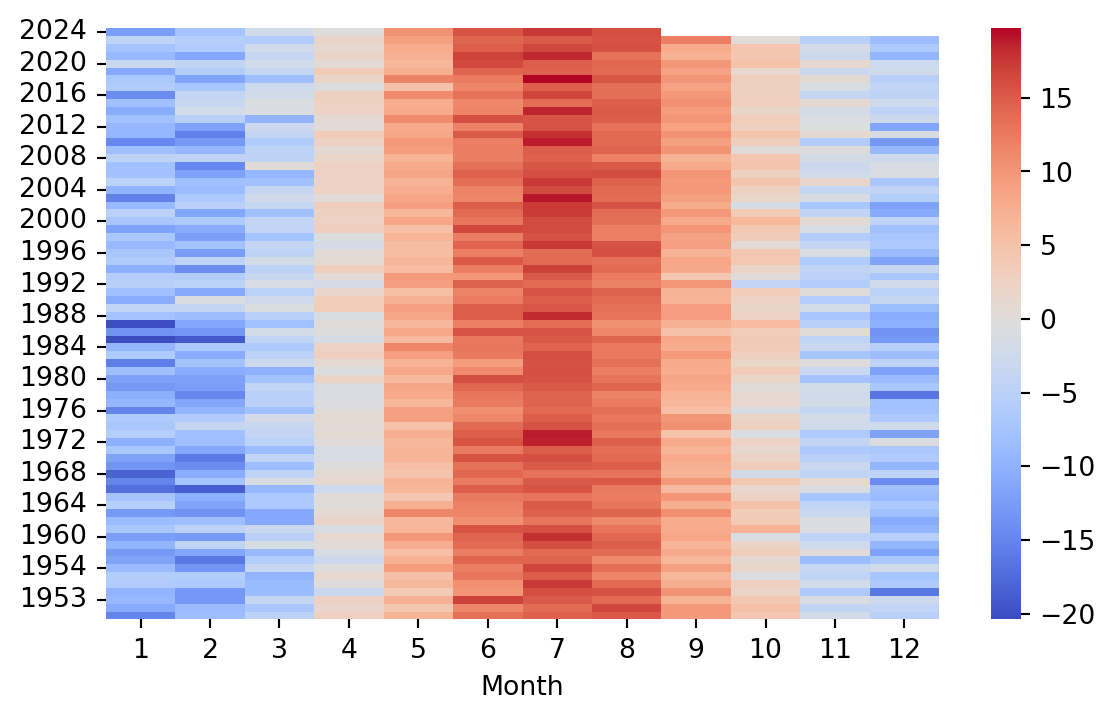

Figure 8.17: Heatmap showing the average temperature in Finland for each month from January of 1950 until August of 2024. Color intensity is used to visualize the temperature values.

8.6 Visualizing Regression

Seaborn is designed for statistical data visualization. With this in mind, it is not that surprizing to learn that Seaborn offers many convenient ways to visualize regression models. The lmplot() and the regplot() functions are the two function offered by Seaborn to visualize a linear fit. You can refer to the Seaborn documentation about the differences between the two functions, but briefly the lmplot() function requires the data argument to be passed, whereas regplot() can be used for plotting e.g. two numpy arrays. Figure 8.18 shows an example of the lmplot() function with the penguins dataset, and Figure 8.19 shows an example of the regplot() function with two numpy arrays.

sns.lmplot(x='flipper_length_mm', y='body_mass_g', data=penguins)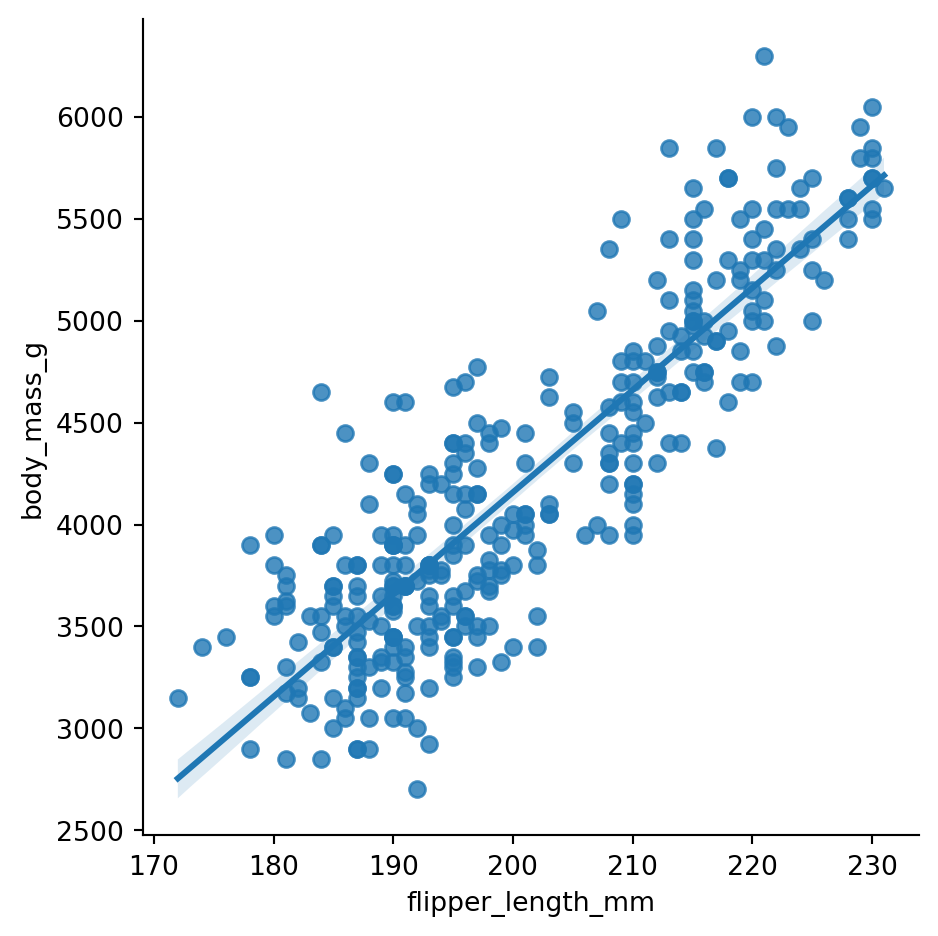

Figure 8.18: The linear relationship between flipper length and body mass of penguins.

# regplot example for numpy arrays
sns.regplot(x=np.random.normal(size=10), y=np.random.normal(size=10))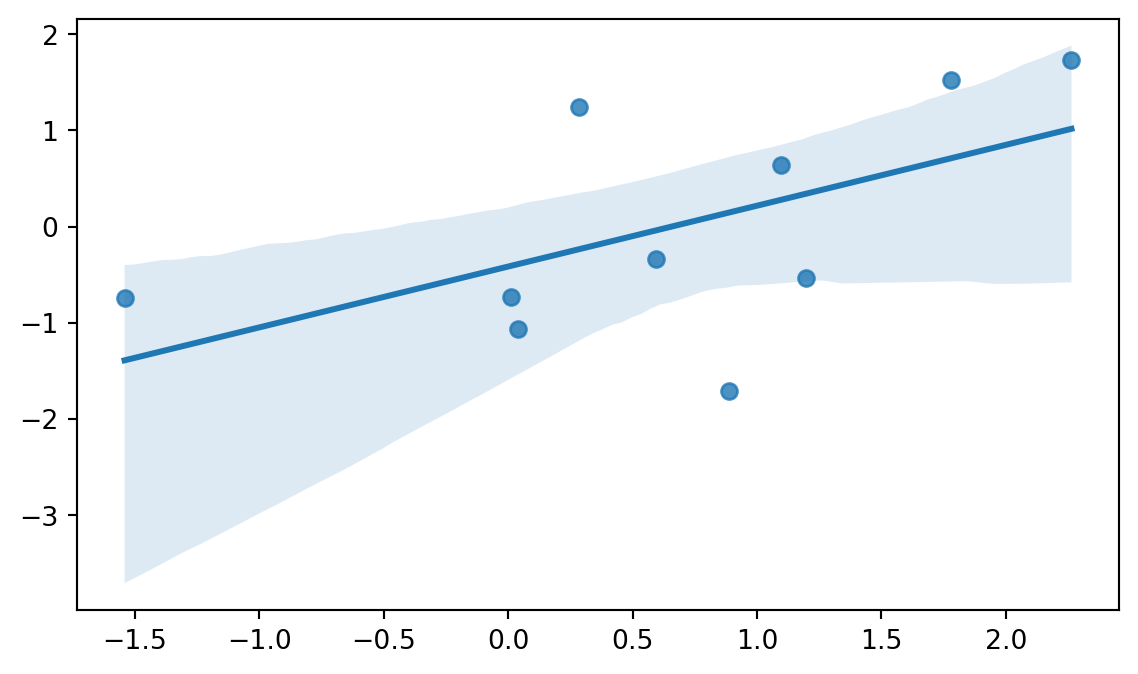

Figure 8.19: The relationship between two random numpy arrays, with a line fitted through the data.

So, as we can see, both functions offer a way to visualize the linear relationship between two variables.

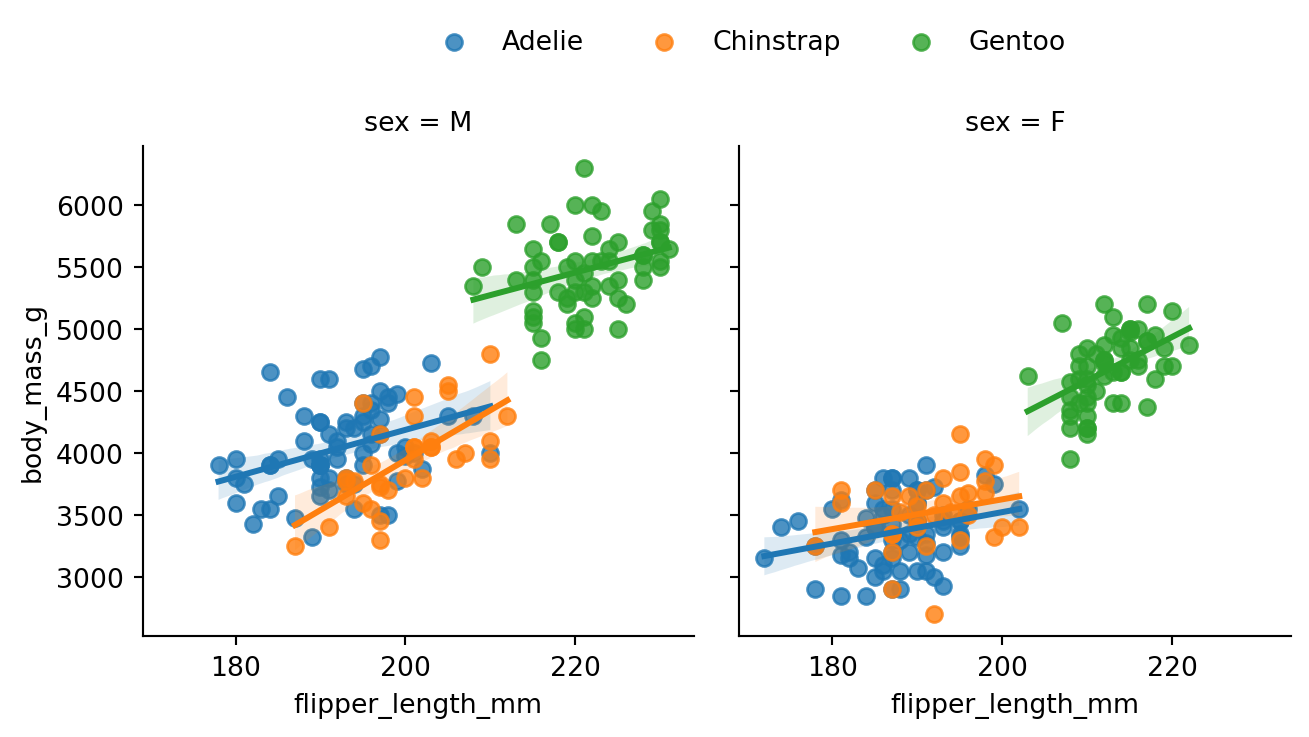
We can utilize similar techniques we saw earlier with the lmplot() and regplot() functions. For example, we can use the hue parameter to color the points based on the species of the penguin, and facet according to sex (Figure 8.20).

g = sns.lmplot(data=penguins, x='flipper_length_mm', y='body_mass_g', 
  hue='species', col='sex', 
  aspect=1, height=3.5
  )
sns.move_legend(g, "lower center",
    bbox_to_anchor=(.5, 1), ncol=3, title=None, frameon=False
    )

Figure 8.20: The linear relationship between flipper length and body mass of penguins separated by sex, where a individual linear fits have been made for each species.

8.6.1 Beyond the linear fit

The lmplot() function is not limited to fitting straight lines. In fact, we can use the order parameter to fit a polynomial regression model. Figure 8.21 demonstrates fitting a second order polynomial to the penguins data.

sns.lmplot(x='flipper_length_mm', y='body_mass_g', data=penguins, order=2)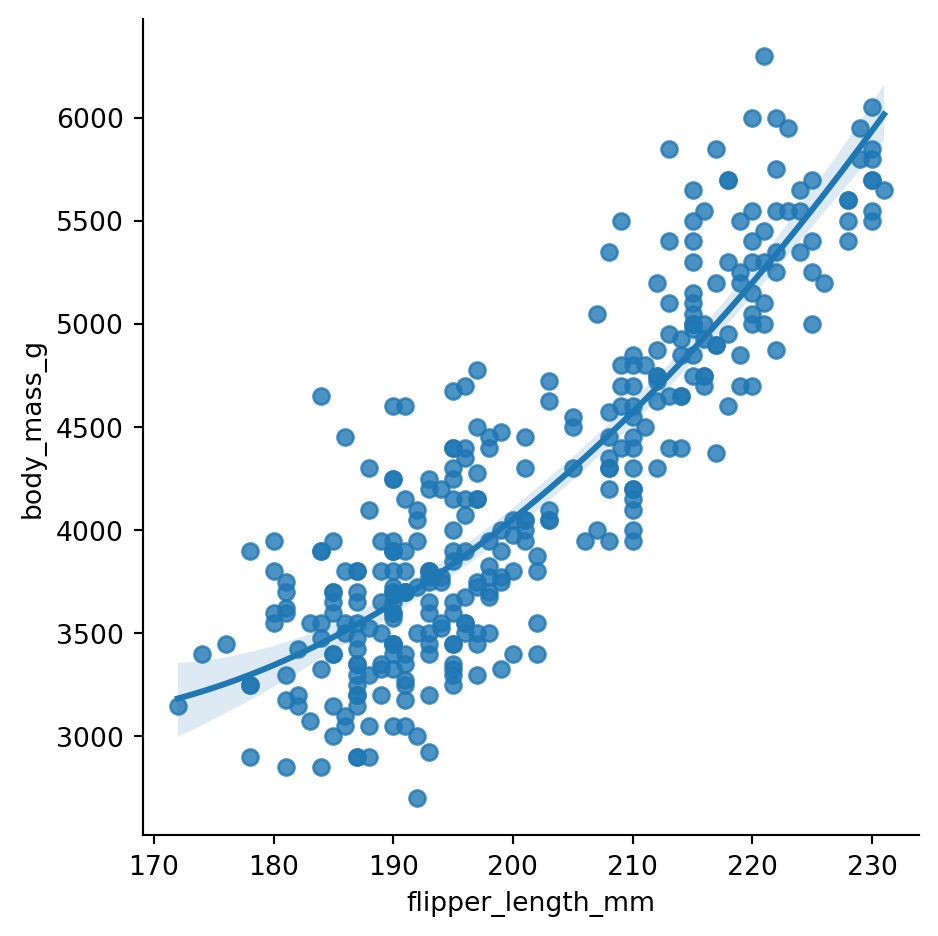

Figure 8.21: A second degree polynomial has been fitted to the flipper length and body mass data.

Logistic regression models are used in binary classification tasks. The logistic curve is characterized by a shape resembling the letter S. We will learn more about logistic regression in the upcoming section. For now, let’s fit a logistic regression model to the penguins data, and see how we can create a visualization to help distinguish between Male and Female Gentoo penguins. We can use the logistic parameter to fit a logistic model after we recode the Male and Female classes to 1 and 0, respectively (Figure 8.22).

# recoding the sex column to be 1 for males and 0 for females
penguins['sex'] = penguins['sex'].apply(lambda x: 1 if x == 'M' else 0)
log_data = penguins[penguins['species'] == 'Gentoo']

sns.lmplot(data = log_data, x='body_mass_g', y='sex', logistic=True,
  height=4, aspect=1.5)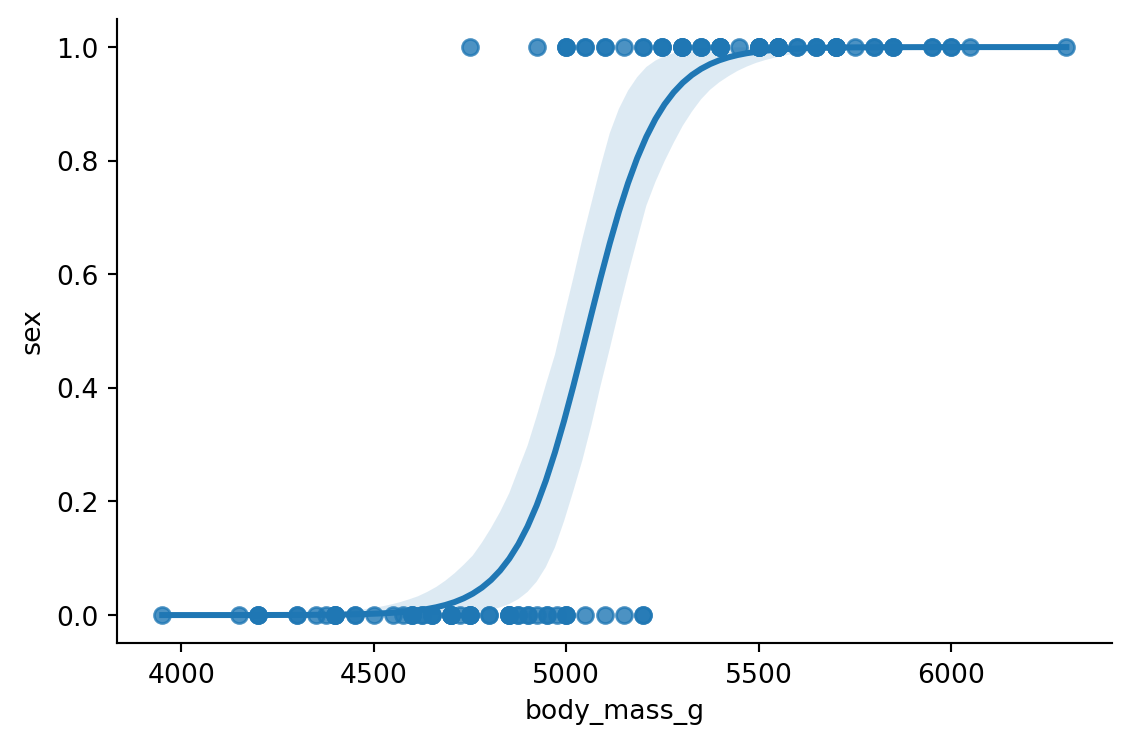

Figure 8.22: A logistic regression fit depicting sex and a function of body mass for Gentoo penguins.

8.7 Conclusion

There are many more functions and features in Seaborn that we are yet to cover. Luckily, we will be using Seaborn in the upcoming section to create visualizations useful for different modelling tasks. This will give us a chance to explore more of Seaborn’s capabilities. Furthermore, you can always refer to the Seaborn documentation for more information.